Gitti und ich bleiben wie angewurzelt vor einem Bild stehen. „Das hängt zu hoch“, sage ich. Gitti nickt zustimmend. Wortlos recken wir beide die Arme nach vorne und zeigen uns gegenseitig, wie tief das Bild hängen müsste. Wir sind uns einig. Ebenso wortlos schütteln wir nun unsere Köpfe, drehen uns um und gehen weiter.
Das geht uns andauernd so! Jedes Bild hat nämlich eine Art Horizont. Das ist auch so, wenn nicht explizit eine Landschaft mit Horizont abgebildet ist. Selbst bei abstrakten Bildern gibt es so etwas wie einen Horizont. Wenn der gefühlt so ungefähr eine Handbreit unterhalb meiner Augen liegt, dann empfinde ich eine gewisse Harmonie. Das hängt natürlich auch davon ab, in welcher Entfernung ich stehe. Es gibt da so eine Distanz, die ich automatisch einnehme, wenn ich ein Bild betrachte. Und die hat vermutlich mit genau diesem Gefühl der Harmonie etwas zu tun. Na ja, und etwas damit, wie groß das Bild und das abgebildete Motiv sind. Es bringt nichts, wenn ich ganz weit weg stehen muss, dann aber selbst mit zusammengekniffenen Augen nichts mehr erkennen kann!
Gitti und ich sind nicht gleich groß. Wir sind sogar unterschiedlich lang. Das ist nicht dasselbe! Meine Mutter zum Beispiel war in unserer Familie unangefochten die Größte, obwohl alle anderen Familienmitglieder etwas länger geraten waren als sie. Zum Glück ist der Längenunterschied zwischen Gitti und mir nicht zu groß, sonst wäre es schwierig, eine für uns beide angenehme Höhe für die Bildhorizonte in unserem Zuhause zu finden. Bei anderen Horizonten, dem geistigen zum Beispiel, ist es auch hilfreich, wenn der nicht zu weit auseinanderliegt. Aber das ist eine andere Geschichte.
Nochmal zum Bildhorizont. Ich strecke also meinen Arm ganz gerade aus, winkle die Hand ab und drehe sie so, dass die Handkante parallel zum Horizont liegt. Wenn sich dann der gefühlte Horizont des Bildes mit meiner Handkante deckt, bin ich zufrieden. Und die Handbreit von vorhin? Die ergibt sich aus dem Abstand zwischen der Höhe meiner Schultern zur Höhe, auf der meine Augen liegen und der Länge meines Armes. Ich könnte mich sofort ein bisschen in der Kunst der Trigonometrie verirren, aber das erspare ich uns. Stattdessen strecke ich einfach den anderen Arm auch noch aus. Die Hand dieses Arms lege ich jetzt einfach oben auf die andere Hand. Beide Daumen zeigen nach unten. Alle Leute um mich herum zeigen jetzt ebenfalls, und zwar mit dem Finger auf mich. Egal, da müssen wir jetzt durch!
Gucke ich geradeaus, sehe ich die obere Handkante. Gucke ich über die Handkante der unteren Hand, möchte ich genau dort den Horizont des Bildes sehen, denn in dieser Position sind meine Augen optimal entspannt. Wir gucken meistens nicht parallel zum Untergrund und stur geradeaus, sondern eben ein kleines Stück nach unten. Weil es weniger anstrengend ist! Wer will schon angestrengt ein Bild anstarren? Also, ich nicht!!
Hui, welch ein Ausflug!
Wer schon einmal versucht hat, Menschen zu zeichnen, weiß, wie schwer das mit den Proportionen ist. Dabei gibt es faszinierend viele Anhaltspunkte. Bei den meisten Menschen sind zum Beispiel die Füße so lang, wie die Unterarme. Zur Sicherheit schlüpfe ich aus dem Schuh, winkle mein Bein ab, ziehe es zu mir heran und halte den Fuß an meinen Unterarm. Die Ferse fest am Ellbogen arretiert, reichen meine Zehen bis zur Handwurzel. Dann verliere ich fast das Gleichgewicht. Gitti guckt mich irritiert an, hält sich aber mit Kommentaren zurück.
Und wo liegt jetzt der ominöse Horizont auf dem Bild selbst? Hat das etwas mit dem Goldenen Schnitt zu tun? Ich krame in meinem Gedächtnis.
Beim Goldenen Schnitt geht es um das Teilungsverhältnis einer Strecke. Der Mathematiker rechnet mir vor: (a+b)/a = a/b und die ganze Strecke ist a+b lang. Ich rechne ein wenig herum, löse die quadratische Gleichung, zu der die Aufgabe führt und erhalte für das Verhältnis von a zu b den ungefähren Wert von 1,618. Die restlichen Nachkommastellen vergesse ich sofort wieder, zumal das unendlich viele sind. Das Ergebnis ist nämlich eine irrationale Zahl. Hihi, „irrational“ finde ich in diesem Zusammenhang besonders schön!
Wenn ein Künstler den Horizont eines Bildes so positioniert, dass der Abstand vom Horizont zum oberen Bildrand etwa 1,6 Mal größer ist, als der zum unteren Bildrand, dann darf er sich schon mal darauf freuen, dass die Betrachter seines Bildes diese Aufteilung wahrscheinlich als harmonisch wahrnehmen werden. Ob ihnen der Rest des Bildes auch gefallen wird, ist nicht gewiss. Will der Künstler das Verhältnis des Goldenen Schnitts exakt treffen, so kann er das auch sauber mit Zirkel und Lineal konstruieren. Handwerker und Künstler haben zumindest früher häufig sogenannte Reduktionszirkel benutzt. Das sind spezielle Zirkel, die auf dieses magische Verhältnis fest eingestellt sind und einem die geometrische Konstruktion abnehmen.
Sind Dinge im Verhältnis des Goldenen Schnitts aufgeteilt, meldet sich unser Sinn für Ästhetik und findet es schön. Weil das so ist, haben viele Leute versucht, ganz viel Bedeutung hineinzugeheimnissen. Sie haben viele Beispiele in der Natur gefunden und daraus die tollsten Schlüsse gezogen. Unabhängig davon, ob sie damit Recht haben oder nicht: Der Goldene Schnitt ist faszinierend. Er funktioniert nicht nur auf Längen bezogen. Man kann auch einen Goldenen Winkel ableiten, also den Umfang eines Kreises im Verhältnis des Goldenen Schnitts teilen und gucken, welcher Winkel sich ergibt. Es gibt Pflanzen, deren Blätter in diesem Winkel zueinander angeordnet sind. Wie viele Blätter es auch sein mögen, sie werden sich niemals vollständig überdecken, weil wir es eben mit einer irrationalen Zahl zu tun haben.
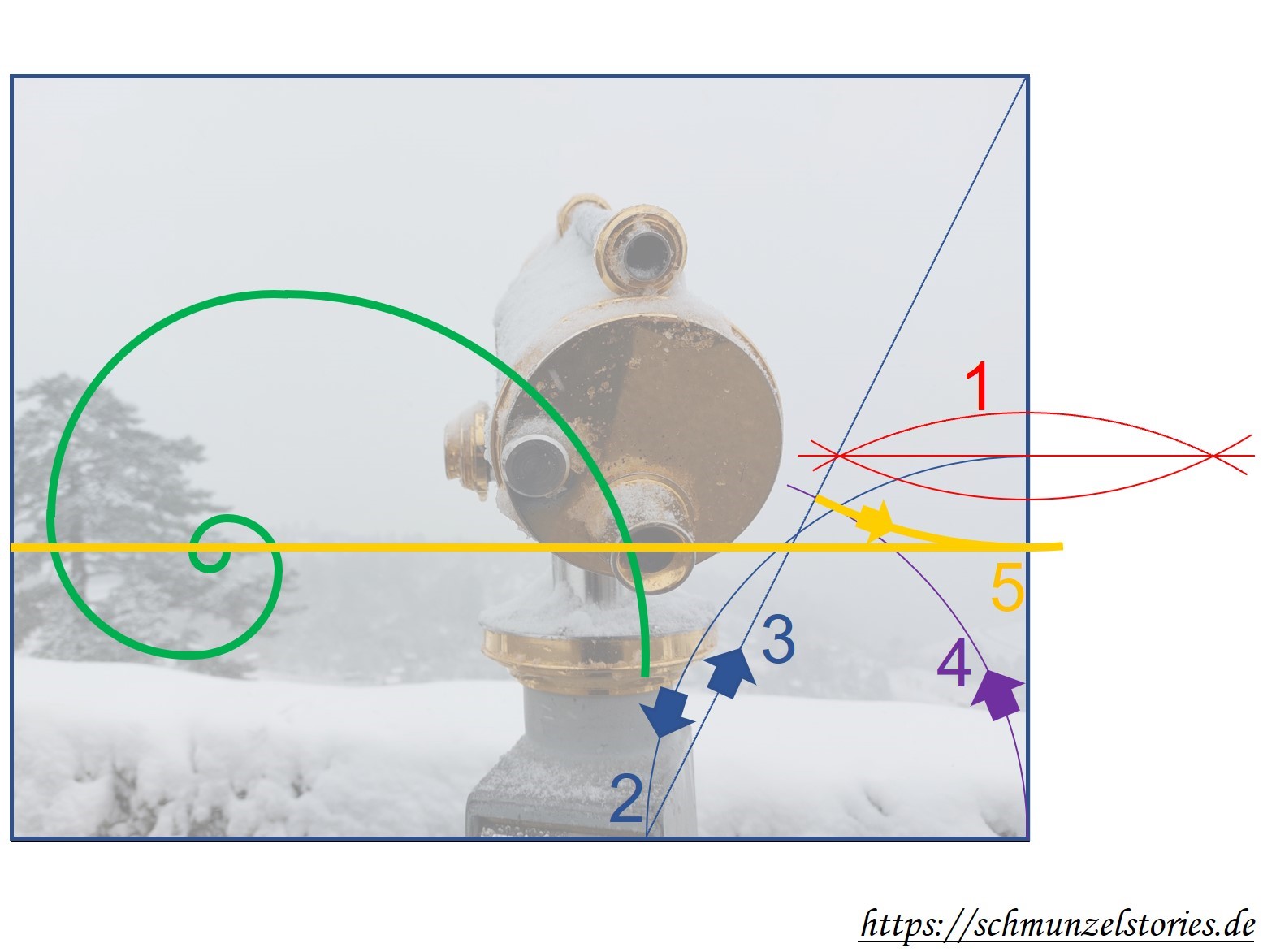
Bei Sonnenblumen begegnet uns schließlich auch noch der italienische Mathematiker Fibonacci mit seiner berühmten Zahlenfolge. Dabei ist jede Zahl die Summe der beiden vorausgehenden Zahlen: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 … Und wenn man die aufeinanderfolgenden Zahlen durcheinander teilt, dann nähert sich das Ergebnis immer mehr dem Goldenen Schnitt an. Schon 21 geteilt durch 13 liegt mit 1,61538 recht nah dran, bei 89 durch 55 kommt 1,61818 raus und so geht es munter weiter. Wenn man dann Viertelkreise mit den Radien der Fibonacci-Folge aneinanderhängt, bekommt man eine angenäherte Spirale. Und jetzt guck Dir mal die Fruchtstände der Sonnenblume an. Ja, die dunklen Dinger da in der Mitte. Die sind in solch einem Spiralmuster angeordnet.
Es gibt ernsthafte Leute, die mal nachgerechnet und ihre Ergebnisse mit ganz vielen echten Sonnenblumen verglichen haben. Was muss das am Ende für ein Gefühl gewesen sein, dass die berechnete Position der Blütenstände nie um mehr als 0,01% von der realen Position abwich? Bei tausend Sonnenblumen! Ich stelle mir ein Feld mit tausend Sonnenblumen vor. Begeistert stünde ich davor, das typische spiralförmige Muster würde ich erkennen. Und ich würde staunen, wie genial die Natur ist, die dafür gesorgt hat, dass sich die vielen Blätter nie vollständig überdecken werden. Kein einziges Blatt wird später ganz im Schatten eines anderen liegen. Aber das Muster nachrechnen? Das käme mir dann doch nicht in den Sinn. Zum Glück gibt es Leute, die dafür einen Sinn haben! Und später würde mir vielleicht einmal einfallen, wozu ich das gerade brauchen kann.